Ploygon Union Contour Lines

Description:

N polygons are placed randomly, with the number of sides of each polygon (m>=3).

Condition:

The ordered set of coordinates for each polygon vertex is known.

Algorithm:

The union of n polygons contour lines, and elimination of internal island areas.

Code Illustrate:

Python demonstration algorithm and graphical explanation.
This regular-routing algorithm is purely original code and does not reference other sets of geometric algorithms.

Example Image:

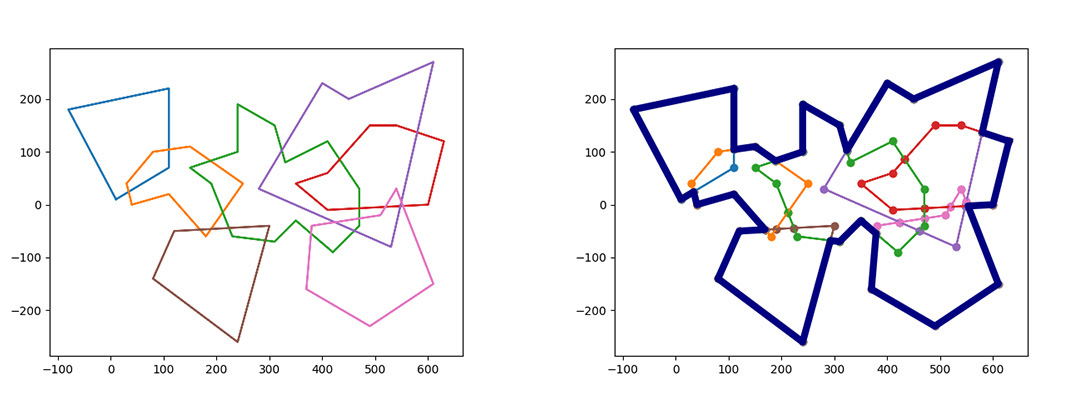
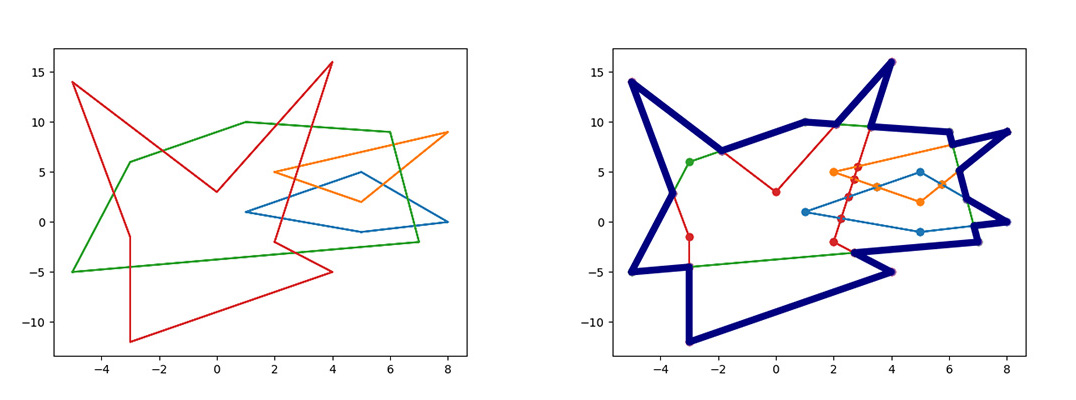
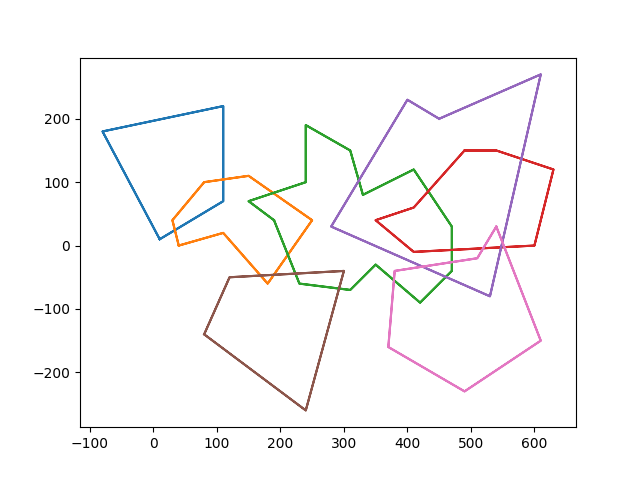
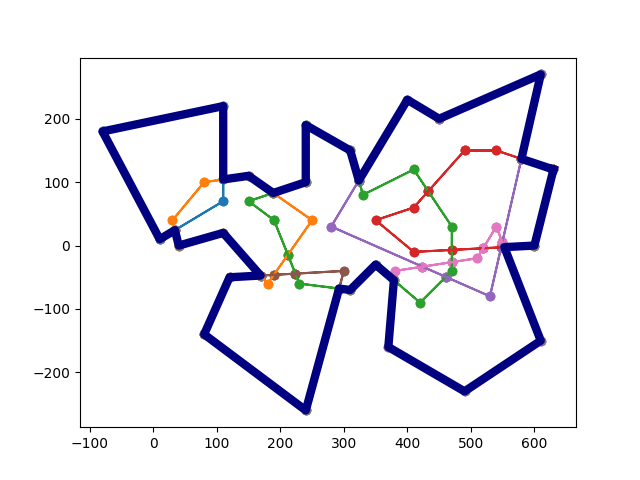
Code：

-- Version 2.0 --

• Spec:
  1- Adaptation of multiple intersections

# --------------------------------------------------------------
#
# Update: 2023.02.17
# Adaptation of multiple intersections
#
# --------------------------------------------------------------

import operator
import numpy as np
from copy import deepcopy
import matplotlib.pyplot as plt
from PloyData_0 import *


def XYMaxPoint(PList):
    Xmax = max(i[0] for i in PList)
    Xlist = []
    for poi in PList:
        if poi[0] == Xmax:
            Xlist.append(poi)
    Ymax = max(i[1] for i in Xlist)
    for i in PList:
        if i[0] == Xmax and i[1] == Ymax:
            return i


def RegulaPloy(ploy):
    Xmax = max([i[0] for i in ploy])
    for id, item in enumerate(ploy):
        if item[0] == Xmax:
            Num = id
            break
    tempPloy = ploy.copy()
    tempPloy.append(ploy[0])
    tempPloy.insert(0, ploy[len(ploy) - 1])
    [x1, y1] = tempPloy[Num]
    [x2, y2] = tempPloy[Num + 1]
    [x3, y3] = tempPloy[Num + 2]
    Wise = (x3 - x2) * (y1 - y2) - (x1 - x2) * (y3 - y2)
    if Wise < 0:
        ploy.reverse()
    return ploy


def SidePloy(ploy):
    SideP = []
    for id, item in enumerate(ploy):
        if id < len(ploy) - 1:
            SideP.append([item, ploy[id + 1]])
        else:
            SideP.append([item, ploy[0]])
    return SideP


# Two line segments intersections
def IsCross(line1, line2):
    [[Ax1, Ay1], [Ax2, Ay2]] = line1
    [[Bx1, By1], [Bx2, By2]] = line2
    m1 = (Bx1 - Ax1) * (Ay2 - Ay1) - (Ax2 - Ax1) * (By1 - Ay1)  # line1 2-sides
    m2 = (Bx2 - Ax1) * (Ay2 - Ay1) - (Ax2 - Ax1) * (By2 - Ay1)
    k1 = (Ax1 - Bx1) * (By2 - By1) - (Bx2 - Bx1) * (Ay1 - By1)  # line2 2-sides
    k2 = (Ax2 - Bx1) * (By2 - By1) - (Bx2 - Bx1) * (Ay2 - By1)
    return m1 * m2 <= 0 and k1 * k2 <= 0


# Find the intersection of two line segments
def CrossPoi(line1, line2):
    [[Ax1, Ay1], [Ax2, Ay2]] = line1
    [[Bx1, By1], [Bx2, By2]] = line2
    Left = (Bx2 - Bx1) * (Ay1 - Ay2) - (Ax2 - Ax1) * (By1 - By2)
    Right = (Ay1 - By1) * (Ax2 - Ax1) * (Bx2 - Bx1) + Bx1 * \
        (By2 - By1) * (Ax2 - Ax1) - Ax1 * (Ay2 - Ay1) * (Bx2 - Bx1)
    x = Right / Left

    Left = (Ax1 - Ax2) * (By2 - By1) - (Ay2 - Ay1) * (Bx1 - Bx2)
    Right = Ay2 * (Ax1 - Ax2) * (By2 - By1) + (Bx2 - Ax2) * \
        (By2 - By1) * (Ay1 - Ay2) - By2 * (Bx1 - Bx2) * (Ay2 - Ay1)
    y = Right / Left
    return [x, y]


def Dis(p1, p2):
    return (p2[0] - p1[0])**2 + (p2[1] - p1[1])**2


# The insertion point is homed to each side
# Determine the order of intersections within each edge
def IndexCrossPoi(ployName, pnum, AllCrossP):
    # Intra-edge intersection collection
    Plist = []
    # All intersections Routing information (including binary and n-forks)）
    for i in AllCrossP:
        if (i[2] == ployName and i[3] == pnum) or (i[4] == ployName and i[5] == pnum):
            Plist.append([i[0], i[1], i[2], i[4]])
    # Add distance information
    for i in Plist:
        i.append(Dis(Data[ployName][pnum], [i[0], i[1]]))
    # Sort
    Plist.sort(key=operator.itemgetter(-1))
    for i in Plist:
        i.pop()
    return Plist


def WiseAngle(v1, v2):
    # v1 rotates to v2, counterclockwise is positive, clockwise is negative
    # Product of 2 vector modulos
    TheNorm = np.linalg.norm(v1) * np.linalg.norm(v2)
    # Multiplication
    rho = np.rad2deg(np.arcsin(np.cross(v1, v2) / TheNorm))
    # Dot
    theta = np.rad2deg(np.arccos(np.dot(v1, v2) / TheNorm))
    if rho < 0:
        theta = -theta
    if theta < 0:
        theta = 360 + theta
    return theta


def GenRoute(Point, VecA):
    # Point Format   [1, 3,  "A","B","F"]
    P0 = [Point[0], Point[1]]
    AngList = []
    for i in range(2, len(Point)):
        ployname = Point[i]
        T = 0
        for poi in Data[ployname]:
            if T == 1:
                PB = poi
                T = 0
                # break
            if poi[0] == Point[0] and poi[1] == Point[1]:
                T = 1
        VecB = [PB[0] - P0[0], PB[1] - P0[1]]
        AngList.append([ployname, WiseAngle(VecA, VecB)])
    AngList.sort(key=operator.itemgetter(-1))
    nextName = AngList[0][0]
    return nextName


def RouteSec(TPoi, StartPoi):
    T = 0
    # Format [X,Y,PloyName]
    ployName = TPoi[2]
    for poi in Data[ployName]:
        if T == 1:
            if poi[0] == StartPoi[0] and poi[1] == StartPoi[1]:
                print("Contour Done！")
                return "OK"
            if len(poi) == 2:
                ContourLine.append([poi[0], poi[1]])
            if len(poi) == 4:
                T = 0
                if poi[2] == ployName:
                    nextName = poi[3]
                elif poi[3] == ployName:
                    nextName = poi[2]
                else:
                    print("Error: Intersection routing information error.")
                return [poi[0], poi[1], nextName]
            # n fork turn
            if len(poi) >= 4 and poi[-1] == "__DoubleCross__":
                T = 0
                poi.pop(-1)
                VecA = [prePoint[0] - poi[0], prePoint[1] - poi[1]]
                nextName = GenRoute(poi, VecA)
                return [poi[0], poi[1], nextName]
            prePoint = poi
        if poi[0] == TPoi[0] and poi[1] == TPoi[1]: 
            # Note Floating-point precision issues
            ContourLine.append([poi[0], poi[1]])
            T = 1
            prePoint = poi


# Generate intersections
def GenCrossPoi():
    PloyPair = []
    KList = [i for i in Data.keys()]
    for i in range(len(KList)):
        for j in range(i + 1, len(KList)):
            PloyPair.append([KList[i], KList[j]])

    AllCrossP = []
    for pair in PloyPair:
        for id, Aline in enumerate(SidePloy(Data[pair[0]])):
            for jd, Bline in enumerate(SidePloy(Data[pair[1]])):
                if IsCross(Aline, Bline):
                    x_y = CrossPoi(Aline, Bline)
                    info = [pair[0], id, pair[1], jd]
                    x_y.extend(info)
                    AllCrossP.append(x_y)

    DCrossP = deepcopy(AllCrossP)
    NCrossPDict = {}
    for id, item in enumerate(DCrossP):
        for jd, jtem in enumerate(DCrossP):
            if jd > id:
                if item[0] == jtem[0] and item[1] == jtem[1]:
                    # 信息分段化
                    key = (item[0], item[1])
                    item0 = []
                    jtem0 = []
                    for i in range(2, len(item) - 1, 2):
                        temp = item[i]
                        item0.append(temp)
                    for j in range(2, len(jtem) - 1, 2):
                        temp = jtem[i]
                        jtem0.append(temp)
                    # 写入分段val
                    if key not in NCrossPDict.keys():
                        NCrossPDict[key] = []
                        for i in item0:
                            NCrossPDict[key].append(i)
                        for j in jtem0:
                            if j not in NCrossPDict[key]:
                                NCrossPDict[key].append(j)
                    for i in item0:
                        if i not in NCrossPDict[key]:
                            NCrossPDict[key].append(i)
                    for j in jtem0:
                        if j not in NCrossPDict[key]:
                            NCrossPDict[key].append(j)
    RepCrossDict = {}
    for key, val in NCrossPDict.items():
        for i in range(len(val)):
            key1 = tuple(list(key))
            RepCrossDict[key1] = list(key) + val + ['__DoubleCross__']
    return DCrossP, RepCrossDict


def plot2D():
    for ploy in Data.values():
        x = [i[0] for i in ploy]
        y = [i[1] for i in ploy]
        x.append(x[0])
        y.append(y[0])
        plt.scatter(x, y)
        plt.plot(x, y)
    x = [i[0] for i in ContourLine]
    y = [i[1] for i in ContourLine]
    x.append(x[0])
    y.append(y[0])
    plt.scatter(x, y)
    plt.plot(x, y, lw=6, color='navy')
    plt.show()


if __name__ == "__main__":
    for val in Data.values():
        val = RegulaPloy(val)
    PlotData = deepcopy(Data)

    AllployPoi = []
    for name, val in PlotData.items():
        for i in val:
            i.append(name)
            AllployPoi.append(i)

    StartPoi = XYMaxPoint(AllployPoi)

    DCrossP, RepCrossDict = GenCrossPoi()

    for name, ploy in Data.items():
        for i in range(len(ploy) - 1, -1, -1):
            insPoiList = IndexCrossPoi(name, i, DCrossP)
            if insPoiList != []:
                insPoiList.reverse()
                for j in insPoiList:
                    ploy.insert(i + 1, j)

    for key, val in RepCrossDict.items():
        for name, ploy in Data.items():
            T = 0
            for i in range(len(ploy) - 1, -1, -1):
                if list(key) == ploy[i][:2] and T == 0:
                    Data[name][i] = val
                    T = 1
                    continue
                if list(key) == ploy[i][:2] and T == 1:
                    Data[name].remove(ploy[i])
                    T = 1

    for key, val in Data.items():
        Data[key] = Data[key] * 2
    Poi_A = StartPoi
    Poi_B = []

    ContourLine = []
    while Poi_B != "OK":
        Poi_B = RouteSec(Poi_A, StartPoi)
        Poi_A = Poi_B

    plot2D()

-- Version 1.2 --

• Spec:
  1- First, regularize the direction of all polygons.
  2- After obtaining the intersection points of the polygons, add routing information.
  3- Reposition all the intersections of the included routing information on each polygon line and regularize again.
  4- From the extreme point of the set, follow the regular edge line from, encounter the intersection point to turn the route sign.
  5- When the starting point is encountered again, the contour line completes the traversal.
  
  
• 说明：
  1- 所有多边形方向正则化
  2- 交点集 加入路由
  3- 路由交点归位至各多边形，再次正则化
  4- 极值点出发，沿正则边线路由。交点按路由标志转向
  5- 遇到出发点，轮廓线完成遍历

# --------------------------------------------------------------
#
# Update: 2023.02.14
#
# --------------------------------------------------------------
import operator
from copy import deepcopy
import matplotlib.pyplot as plt
from PloyData_1 import *


def XYMaxPoint(PList):
    Xmax = max(i[0] for i in PList)
    Xlist = []
    for poi in PList:
        if poi[0] == Xmax:
            Xlist.append(poi)
    Ymax = max(i[1] for i in Xlist)
    for i in PList:
        if i[0] == Xmax and i[1] == Ymax:
            return i


def RegulaPloy(ploy):
    # X-extreme point. The need for regular judgment
    Xmax = max([i[0] for i in ploy])
    for id, item in enumerate(ploy):
        if item[0] == Xmax:
            Num = id
            break
    # Extend the data on both sides
    tempPloy = ploy.copy()
    tempPloy.append(ploy[0])
    tempPloy.insert(0, ploy[len(ploy) - 1])
    # Extend the data on both sides
    [x1, y1] = tempPloy[Num]
    [x2, y2] = tempPloy[Num + 1]
    [x3, y3] = tempPloy[Num + 2]
    Wise = (x3 - x2) * (y1 - y2) - (x1 - x2) * (y3 - y2)
    if Wise < 0:
        ploy.reverse()
    return ploy


def SidePloy(ploy):
    # Generate regular edges
    SideP = []
    for id, item in enumerate(ploy):
        if id < len(ploy) - 1:
            SideP.append([item, ploy[id + 1]])
        else:
            SideP.append([item, ploy[0]])
    return SideP


def IsCross(line1, line2):
    [[Ax1, Ay1], [Ax2, Ay2]] = line1
    [[Bx1, By1], [Bx2, By2]] = line2
    m1 = (Bx1 - Ax1) * (Ay2 - Ay1) - (Ax2 - Ax1) * (By1 - Ay1)  # line1 2-sides
    m2 = (Bx2 - Ax1) * (Ay2 - Ay1) - (Ax2 - Ax1) * (By2 - Ay1)
    k1 = (Ax1 - Bx1) * (By2 - By1) - (Bx2 - Bx1) * (Ay1 - By1)  # line2 2-sides
    k2 = (Ax2 - Bx1) * (By2 - By1) - (Bx2 - Bx1) * (Ay2 - By1)
    return m1 * m2 <= 0 and k1 * k2 <= 0


def CrossPoi(line1, line2):
    [[Ax1, Ay1], [Ax2, Ay2]] = line1
    [[Bx1, By1], [Bx2, By2]] = line2
    Left = (Bx2 - Bx1) * (Ay1 - Ay2) - (Ax2 - Ax1) * (By1 - By2)
    Right = (Ay1 - By1) * (Ax2 - Ax1) * (Bx2 - Bx1) + Bx1 * \
        (By2 - By1) * (Ax2 - Ax1) - Ax1 * (Ay2 - Ay1) * (Bx2 - Bx1)
    x = Right / Left

    Left = (Ax1 - Ax2) * (By2 - By1) - (Ay2 - Ay1) * (Bx1 - Bx2)
    Right = Ay2 * (Ax1 - Ax2) * (By2 - By1) + (Bx2 - Ax2) * \
        (By2 - By1) * (Ay1 - Ay2) - By2 * (Bx1 - Bx2) * (Ay2 - Ay1)
    y = Right / Left
    return [x, y]


def Dis(p1, p2):
    return (p2[0] - p1[0])**2 + (p2[1] - p1[1])**2


def IndexCrossPoi(ployName, ploy, pnum, AllCrossP):
    Plist = []
    for i in AllCrossP:
        if (i[2] == ployName and i[3] == pnum) or (i[4] == ployName and i[5] == pnum):
            Plist.append(i)
    for i in Plist:
        if len(i) == 6:
            i.append(Dis(ploy[pnum], [i[0], i[1]]))
        if len(i) == 7:
            i[6] = Dis(ploy[pnum], [i[0], i[1]])
    Plist.sort(key=operator.itemgetter(6))
    return Plist


def RouteSec(XYRpoi, StartPoi):
    T = 0
    ployName = XYRpoi[2]
    for poi in Data[ployName]:
        if T == 1:
            if poi[0] == StartPoi[0] and poi[1] == StartPoi[1]:
                print("Contour lines are Generated！")
                return "OK"
            if len(poi) == 2:
                ContourLine.append([poi[0], poi[1]])
            if len(poi) > 2:
                T = 0
                if poi[2] == ployName:
                    nextName = poi[4]
                elif poi[4] == ployName:
                    nextName = poi[2]
                else:
                    print("Error: The intersection routing information is incorrect.")
                return [poi[0], poi[1], nextName]
        if poi[0] == XYRpoi[0] and poi[1] == XYRpoi[1]:
            ContourLine.append([poi[0], poi[1]])
            T = 1


def plot2D():
    for ploy in Data.values():
        x = [i[0] for i in ploy]
        y = [i[1] for i in ploy]
        x.append(x[0])
        y.append(y[0])
        plt.scatter(x, y)
        plt.plot(x, y)
    x = [i[0] for i in ContourLine]
    y = [i[1] for i in ContourLine]
    x.append(x[0])
    y.append(y[0])
    plt.scatter(x, y)
    plt.plot(x, y, lw=6, color='navy')
    plt.show()


if __name__ == "__main__":

    # Ploy direction regularization
    for val in Data.values():
        val = RegulaPloy(val)
    PlotData = deepcopy(Data)

    # n polygons, bubbling method Pair two.
    # List numbered index bubbling pairing.
    PloyPair = []
    KList = [i for i in Data.keys()]
    for i in range(len(KList)):
        for j in range(i + 1, len(KList)):
            PloyPair.append([KList[i], KList[j]])

    # Calculate all intersection points.
    AllCrossP = []
    for pair in PloyPair:
        for id, Aline in enumerate(SidePloy(Data[pair[0]])):
            for jd, Bline in enumerate(SidePloy(Data[pair[1]])):
                if IsCross(Aline, Bline):
                    xy = CrossPoi(Aline, Bline)
                    info = [pair[0], id, pair[1], jd]
                    xy.extend(info)
                    AllCrossP.append(xy)

    # Each side intersects point retrieval / insertion
    # Polygon vertex ploy update
    # (with intersection inserts)
    for name, ploy in Data.items():
        for i in range(len(ploy) - 1, -1, -1):
            insPoiList = IndexCrossPoi(name, ploy, i, AllCrossP)
            if insPoiList != []:
                insPoiList.reverse()
                for j in insPoiList:
                    ploy.insert(i + 1, j)

    for key, val in Data.items():
        Data[key] = Data[key] * 2

    # Generate StartPoint
    AllployPoi = []
    for name, val in PlotData.items():
        for i in val:
            i.append(name)
            AllployPoi.append(i)
    StartPoi = XYMaxPoint(AllployPoi)
    Poi_A = StartPoi
    Poi_B = []

    # Generate Contour
    ContourLine = []
    while Poi_B != "OK":
        Poi_B = RouteSec(Poi_A, StartPoi)
        Poi_A = Poi_B

    # Plot
    plot2D()